Eisenstein’s Lattice Point Proof of Quadratic Reciprocity

The Law of Quadratic Reciprocity is a cornerstone of classical number theory—Gauss himself called it the “Theorema Aureum” (Golden Theorem). Although Gauss provided multiple proofs, Eisenstein’s geometric argument simplifies Gauss’s third proof by employing a lattice‐point counting method.

Statement of the Law of Quadratic Reciprocity

Let $p$ and $q$ be distinct odd primes. The Law of Quadratic Reciprocity (QRL) asserts that

$\displaystyle \left(\frac{q}{p}\right)\,\left(\frac{p}{q}\right) \;=\; (-1)^{\frac{p-1}{2}\,\frac{q-1}{2}}.$

We will recall the definition of the Legendre symbol and Euler’s Criterion, then introduce the key sums that Eisenstein uses, and finally carry out the lattice‐point counting argument.

The Legendre Symbol and Euler’s Criterion

For an odd prime $p$ and an integer $a$ , the Legendre symbol $\left(\frac{a}{p}\right)$ is defined by

$\displaystyle \left(\frac{a}{p}\right) = \begin{cases} 1, & \text{if } a \text{ is a quadratic residue modulo } p \text{ and } p \nmid a, \\ -1, & \text{if } a \text{ is a nonresidue modulo } p \text{ and } p \nmid a, \\ 0, & \text{if } p \mid a. \end{cases}$

Euler’s Criterion gives a practical way to compute $\left(\frac{a}{p}\right)$ when $p \nmid a$ .

Criterion 1 (Euler’s Criterion). Let $p$ be an odd prime and let $a$ be an integer with $p \nmid a$ . Then

$\displaystyle \left(\frac{a}{p}\right) \;\equiv\; a^{\frac{p-1}{2}} \pmod{p}.$

Since both sides are $\pm 1$ , this congruence implies actual equality.

Eisenstein’s Key Sums

Throughout this section, set $M = \frac{p-1}{2}$ . We will introduce two sums:

The Eisenstein sum $S_{E}(q,p)$ , which runs over even integers in $\{1,2,\ldots,p-1\}$ .
The geometric sum $\lambda(q,p)$ , which counts lattice points under a certain line.

Eisenstein’s Sum $S_{E}(q,p)$

Define

$\displaystyle S_{E}(q,p) \;=\; \sum_{k=1}^{M} \left\lfloor \frac{q\,(2k)}{p} \right\rfloor.$

Observe that the even integers $2k$ range over $\{2,4,\dots,p-1\}$ . For each such $x=2k$ , the quantity

$\displaystyle \left\lfloor \frac{q\,x}{p} \right\rfloor$

counts the number of integer points $(x,y)$ with $1 \le y \le \frac{q\,x}{p}$ . Hence,

$\displaystyle S_{E}(q,p) \;=\; \sum_{\substack{x=2 \\ x \text{ even}}}^{p-1} \#\Bigl\{\,y \in \mathbb{Z}: 1 \le y \le \tfrac{q\,x}{p}\Bigr\}.$

In other words, $S_{E}(q,p)$ counts all integer lattice points $(x,y)$ satisfying

$\displaystyle x \in \{2,4,6,\dots,p-1\}, \quad 1 \le y < \frac{q\,x}{p}.$

The Geometric Sum $\lambda(q,p)$

Define

$\displaystyle \lambda(q,p) \;=\; \sum_{x=1}^{M} \left\lfloor \frac{q\,x}{p} \right\rfloor.$

Here the summation index $x$ runs over all positive integers $1 \le x \le M = \tfrac{p-1}{2}$ . For each $x$ ,

$\displaystyle \left\lfloor \frac{q\,x}{p} \right\rfloor$

counts the integer points $(x,y)$ with $1 \le y < \tfrac{q\,x}{p}$ . Hence,

$\displaystyle \lambda(q,p) \;=\; \sum_{x=1}^{\,\tfrac{p-1}{2}} \#\Bigl\{\,y \in \mathbb{Z}: 1 \le y < \tfrac{q\,x}{p}\Bigr\}.$

Geometrically, these are exactly the lattice points strictly below the line

$\displaystyle L: \; p\,y = q\,x,$

in the interior of the (half‐height) triangle with vertices

$\displaystyle (0,0), \quad \Bigl(\tfrac{p}{2},\,0\Bigr), \quad \Bigl(\tfrac{p}{2},\,\tfrac{q}{2}\Bigr).$

In the sequel, we will see that $\lambda(q,p)$ is more convenient than $S_{E}(q,p)$ when performing the final lattice‐point count.

Eisenstein’s Lemma

The first major step is to show that the arithmetic definition of $\left(\frac{q}{p}\right)$ can be expressed in terms of the parity of $S_{E}(q,p)$ .

Lemma 1 (Eisenstein). Let $p$ and $q$ be distinct odd primes. Then

$\displaystyle \left(\frac{q}{p}\right) \;=\; (-1)^{\,S_{E}(q,p)}.$

Proof Sketch.

Let
$\displaystyle E \;=\; \{\,2, \,4, \,6, \dots, p-1\}$
be the set of all $M = \tfrac{p-1}{2}$ even residues modulo $p$ . For each $u \in E$ , write
$\displaystyle q\,u \;\equiv\; r_u \pmod{p}, \quad 1 \le r_u \le p-1.$
Notice that $r_u$ is some residue in $\{1,2,\dots,p-1\}$ . Now define
$\displaystyle r'_u := \begin{cases} r_u, & \text{if } r_u \text{ is even},\\ p - r_u, & \text{if } r_u \text{ is odd}. \end{cases}$
Since $r_u < p$ , if $r_u$ is odd then $p - r_u$ is even. Hence $\{r'_u\}$ runs over exactly the same set $E$ , just permuted.
Observe the congruence
$\displaystyle q\,u \;\equiv\; \begin{cases} r_u, & \text{if } r_u \text{ is even},\\ -\,r'_u, & \text{if } r_u \text{ is odd}. \end{cases}$
Equivalently,
$\displaystyle q\,u \;\equiv\; (-1)^{\,r_u \bmod 2}\,r'_u \pmod{p}.$
Taking the product over all $u \in E$ yields
$\displaystyle q^{M}\,\prod_{u \in E} u \;\equiv\; (-1)^{\sum_{u \in E} (r_u \bmod 2)} \,\prod_{u \in E} r'_u \pmod{p}.$
But $\{r'_u : u \in E\}$ is a permutation of $E$ , so $\prod_{u \in E} r'_u = \prod_{u \in E} u$ . Since neither product is divisible by $p$ , we cancel $\prod_{u \in E} u$ from both sides to obtain
$\displaystyle q^{M} \;\equiv\; (-1)^{\sum_{u \in E} (r_u \bmod 2)} \pmod{p}.$
By Euler’s Criterion, $\displaystyle \left(\frac{q}{p}\right) \equiv q^{M} \pmod{p}$ when $p \nmid q$ . Thus
$\displaystyle \left(\frac{q}{p}\right) = (-1)^{\sum_{u \in E} (r_u \bmod 2)}$
Finally, relate $r_u \bmod 2$ to $\left\lfloor q\,u / p \right\rfloor$ . Since $u$ is even, $q\,u$ is even. Write
$\displaystyle q\,u = p \,\left\lfloor \tfrac{q\,u}{p} \right\rfloor + r_u.$
Here $p\,\left\lfloor \tfrac{q\,u}{p} \right\rfloor$ is odd or even according to whether $\left\lfloor \tfrac{q\,u}{p} \right\rfloor$ is odd or even, because $p$ itself is odd. But the left‐hand side $q\,u$ is even, so $r_u$ must have the same parity as $\left\lfloor \tfrac{q\,u}{p} \right\rfloor$ . In symbols:
$\displaystyle r_u \equiv \left\lfloor \tfrac{q\,u}{p} \right\rfloor \pmod{2}.$
Therefore,
$\displaystyle \sum_{u \in E} (r_u \bmod 2) \equiv \sum_{u \in E} \left\lfloor \tfrac{q\,u}{p} \right\rfloor = S_{E}(q,p) \pmod{2}.$
Combining these congruences shows
$\displaystyle \left(\frac{q}{p}\right) = (-1)^{\,S_{E}(q,p)},$
completing the proof of the lemma.

Q.E.D.

From $S_{E}(q,p)$ to $\lambda(q,p)$

Eisenstein’s next insight is that, modulo 2, the sum over even $x$ (namely $S_{E}(q,p)$ ) is congruent to the sum over all $x = 1,2,\dots,\tfrac{p-1}{2}$ , i.e. $\lambda(q,p)$ . We give a streamlined parity argument that shows

$\displaystyle S_{E}(q,p) \;\equiv\; \lambda(q,p) \pmod{2}.$

Relating Even‐ $x$ Points to Odd‐ $x$ Points

Recall

$\displaystyle S_{E}(q,p) = \sum_{k=1}^{M} \left\lfloor \frac{q\,(2k)}{p} \right\rfloor, \quad x = 2k \in \{2,4,6,\dots,p-1\}.$

Fix a particular even line $x = 2k$ . On that vertical line, all integer lattice points have coordinates $(2k,y)$ with $y = 1,2,\dots,q-1$ . Since $q$ is odd, $q-1$ is even, so there are exactly $q-1$ points on that vertical line between $y=1$ and $y=q-1$ .

The number of points strictly below the line $L: y = \tfrac{q\,x}{p}$ is
$\displaystyle \left\lfloor \tfrac{q\,(2k)}{p} \right\rfloor.$
The number of points strictly above $L$ (but with $1 \le y \le q-1$ ) is
$\displaystyle (q-1) \;-\; \left\lfloor \tfrac{q\,(2k)}{p} \right\rfloor.$

Since $q-1$ is even, it follows that

$\displaystyle \left\lfloor \tfrac{q\,(2k)}{p} \right\rfloor \;\equiv\; (q-1) - \left\lfloor \tfrac{q\,(2k)}{p} \right\rfloor \quad(\bmod 2).$

We can see that

$\displaystyle (q - 1) - \left\lfloor \tfrac{q\,(2k)}{p} \right\rfloor \;=\; \left\lfloor \tfrac{q\,\bigl(p - 2k\bigr)}{p} \right\rfloor,$

where $p - 2k$ is an odd integer in $\{1,3,5,\dots,p-2\}$ . Concretely, each point above the line $L$ on the even column $x=2k$ corresponds to a unique point below $L$ on the odd column $x = p - 2k$ . Hence, for each $k$ ,

$\displaystyle \left\lfloor \tfrac{q\,(2k)}{p} \right\rfloor \;\equiv\; \left\lfloor \tfrac{q\,\bigl(p - 2k\bigr)}{p} \right\rfloor \quad(\bmod 2).$

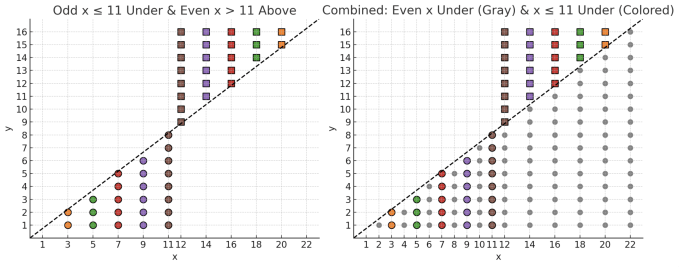
Comparing to $\lambda(q,p)$

Now break the sum

$\displaystyle \lambda(q,p) = \sum_{x=1}^{M} \left\lfloor \tfrac{q\,x}{p} \right\rfloor$

into two parts: one over odd $x$ and one over even $x$ . That is,

$\displaystyle \lambda(q,p) = \sum_{\substack{x=1 \\ x \text{ odd}}}^{M} \left\lfloor \tfrac{q\,x}{p} \right\rfloor \;+\; \sum_{\substack{x=1 \\ x \text{ even}}}^{M} \left\lfloor \tfrac{q\,x}{p} \right\rfloor.$

Observe that the sum over odd $x$ in the range $1 \le x \le M = \tfrac{p-1}{2}$ is exactly

$\displaystyle \sum_{\substack{x = 1 \\ x \text{ odd}}}^{M} \left\lfloor \tfrac{q\,x}{p} \right\rfloor \;=\; \sum_{\substack{x = 1 \\ u=p-x \text{ even}}}^{M} \left\lfloor \tfrac{q\,u}{p} \right\rfloor \quad(\bmod 2).$

which after reindexing matches

$\displaystyle \sum_{\substack{x = \frac{p+1}{2} \\ x \text{ even}}}^{p-1} \left\lfloor \tfrac{q\,x}{p} \right\rfloor \quad(\bmod 2).$

Hence

$\displaystyle \lambda(q,p) \equiv \sum_{\substack{x=1 \\ x \text{ even}}}^{p-1} \left\lfloor \tfrac{q\,x}{p} \right\rfloor \;=\; S_{E}(q,p) \quad(\bmod 2).$

Since $\left(\frac{q}{p}\right) = (-1)^{S_{E}(q,p)}$ , we conclude

$\displaystyle \left(\frac{q}{p}\right) = (-1)^{\lambda(q,p)}.$

The Main Geometric Counting Argument

We have now re‐expressed

$\displaystyle \left(\frac{q}{p}\right) = (-1)^{\lambda(q,p)}, \qquad \left(\frac{p}{q}\right) = (-1)^{\lambda(p,q)},$

where

$\displaystyle \lambda(q,p) = \sum_{x=1}^{(p-1)/2} \left\lfloor \frac{q\,x}{p} \right\rfloor, \quad \lambda(p,q) = \sum_{y=1}^{(q-1)/2} \left\lfloor \frac{p\,y}{q} \right\rfloor.$

We now count all integer points $(x,y)$ in the rectangle

$\displaystyle \mathcal{R} = \Bigl\{ (x,y)\in\mathbb{R}^2 : 0 < x < \tfrac{p}{2}, \; 0 < y < \tfrac{q}{2} \Bigr\},$

with $x,y\in\mathbb{Z}$ . Precisely, we consider

$\displaystyle \bigl\{ (x,y)\in\mathbb{Z}^2 : 1 \le x \le \tfrac{p-1}{2}, \; 1 \le y \le \tfrac{q-1}{2} \bigr\}.$

Since there are $\tfrac{p-1}{2}$ choices for $x$ and $\tfrac{q-1}{2}$ choices for $y$ , the total number of such lattice points is

$\displaystyle N_{\text{total}} = \frac{p-1}{2} \times \frac{q-1}{2}.$

No such lattice point $(x,y)$ lies exactly on the line

$\displaystyle L: p\,y = q\,x,$

because if $p\,y = q\,x$ and $1 \le x \le \tfrac{p-1}{2}$ , then $p \mid q\,x$ . Since $p$ and $q$ are distinct primes, $p \nmid q$ , so $p$ must divide $x$ . But $0 < x < p$ forces $x=0$ , which is impossible in our index range. Hence all lattice points in $\mathcal{R}$ are either strictly below $L$ or strictly above $L$ .

The points strictly below $L$ (i.e. satisfying $p\,y < q\,x$ ) are counted by
$\displaystyle \lambda(q,p) = \sum_{x=1}^{(p-1)/2} \#\Bigl\{\,y : 1 \le y < \tfrac{q\,x}{p}\Bigr\} = \sum_{x=1}^{(p-1)/2} \left\lfloor \tfrac{q\,x}{p} \right\rfloor.$
The points strictly above $L$ (i.e. satisfying $p\,y > q\,x$ ) are counted by
$\displaystyle \lambda(p,q) = \sum_{y=1}^{(q-1)/2} \#\Bigl\{\,x : 1 \le x < \tfrac{p\,y}{q}\Bigr\} = \sum_{y=1}^{(q-1)/2} \left\lfloor \tfrac{p\,y}{q} \right\rfloor.$

Since these two sets of points partition all $N_{\text{total}}$ lattice points in $\mathcal{R}$ , we have

$\displaystyle \lambda(q,p) + \lambda(p,q) = N_{\text{total}} = \frac{p-1}{2} \cdot \frac{q-1}{2}.$

Therefore,

$\displaystyle \left(\frac{q}{p}\right)\,\left(\frac{p}{q}\right) = (-1)^{\lambda(q,p)}\,(-1)^{\lambda(p,q)} = (-1)^{\lambda(q,p) + \lambda(p,q)} = (-1)^{\frac{p-1}{2} \,\frac{q-1}{2}}.$

This completes Eisenstein’s geometric proof of the Law of Quadratic Reciprocity.

Concluding Remarks

The beauty of this argument lies in translating an arithmetic statement about Legendre symbols into a purely geometric enumeration problem.
Eisenstein’s parity argument shows that summing over even $x$ -coordinates (the original sum $S_{E}(q,p)$ ) is congruent mod 2 to summing over all $1 \le x \le (p-1)/2$ . This relates the parity of the Eisenstein sum to a sum more geometric.
The final step is a simple but elegant lattice‐point count in a rectangle, divided by a diagonal line of slope $q/p$ . No point in the interior can lie exactly on the diagonal, ensuring that every point is counted either “below” or “above.”

Statement of the Law of Quadratic Reciprocity

The Legendre Symbol and Euler’s Criterion

Eisenstein’s Key Sums

Eisenstein’s Sum

The Geometric Sum

Eisenstein’s Lemma

From to

Relating Even‐ Points to Odd‐ Points

Comparing to